
The symmetrical qualities of the circle are frequently used by architects when designing sports tracks, recreational parks, buildings, roundabouts, Ferris wheels, and other structures. Mathematicians studied circles, which helped them develop calculus and astronomy. As there was no idea of 3D shapes, people assumed that the moon, sun, and other planets were circular. The circle has a long and illustrious history. A circle should never be confused with a polygon because it is made up of curves instead of straight lines.
A circle is a perfectly round or closed, two-dimensional geometrical shape described as a set of all points in the plane equidistant from a particular central point. So, the measure of angle with vertex outside the circle is 50°.The term “circle” comes from the Latin word circus, which means hoop or ring. Now you need to recall the properties we studied above. Given the intercepted arcs as 62° and 150°įind the external vertex angle in the diagram shown below. If the intercepted arc in the diagram below is 160°, determine the value of x.įind the value of the inscribed angle in the following diagram.įind the value of x in the diagram shown below. Therefore, the measure of the intercepted arc is 30°. The inscribed angle = ½ × intercepted arc Worked out examples about the intercepted arc.įind angle ABC in the circle shown below.ĭetermine the value of x in the circle shown below.įind the value of the intercepted arc in the diagram shown below. The size of the vertex angle outside the circle = 1/2 × (difference of intercepted arcs) The inscribed angle = half the sum of intercepted arcs. The inscribed angle = 1/2 × intercepted arcĢ x the inscribed angle = the intercepted arcįor intersecting chords, the intercepted arc is given by,

The central angle = the measure of the intercepted arc Intercepted arc formula for lines meeting in the middle of a circle.These relationships between different intercepted arcs and their corresponding inscribed angles form the intercepted arc formula. The central angle is an angle formed by two radii that joins the ends of a chord to the center of a circle. In geometry, an inscribed angle is formed between the chords or lines cutting across a circle. There exist some interesting relationships between an intercepted arc and the inscribed and central angle of a circle.
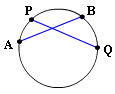
Or we can also define the intercepted arc as when two lines cross a circle at two different points, the part of the circle between the points of intersection forms the intercepted arc. It is important to note that the lines or the chords can either meet in the middle of a circle, on the other side of a circle or outside a circle. An intercepted arc can therefore be defined as an arc formed when one or two different chords or line segments cut across a circle and meet at a common point called a vertex. To recall, an arc is part of the circumference of a circle. We saw all the basic definitions of parts of circles before, like diameter, chord, vertex, and central angle if you have not, please go through the previous lessons because these parts have a use in this lesson. If you are really good at angles, then this lesson should not be a problem for you to understand. We are talking about the intercepted arc, which is formed in the circle due to external lines. Now that we have learned all the basic parts of the circle let’s go into something complex.


 0 kommentar(er)
0 kommentar(er)
